Blockchains, banks and zero-knowledge proofs

Open and decentralised systems such as blockchains create privacy concerns for some use cases, made even more acute by permissioned blockchains which seem to be morphing into something that belies almost all the fundamental benefits of the original design – but that's another story.

Ensuring privacy of transaction data is a desirable feature at the very least, and probably the sine qua non of distributed banking ledgers. Heavy hitters in the blockchain space such as Ethereum's Vitalik Buterin and Chain.com's Adam Ludwin are enthusiastic about the potential of zero-knowledge proofs, which truthfully prove properties of encrypted data without revealing the data itself.

Professor Eli Ben-Sasson of Technion, Israel Institute of Technology is an expert on zero-knowledge (ZK) proofs and part of the Zerocash project and the startup Zcash. There's a big difference between ZK proofs and almost all currently used cryptography, such as hashing, public key cryptography and digital signatures.

These traditional cryptography methods are very good at dealing with data, said Ben-Sasson. "You can sign a file, you can encrypt a file, you can hash and commit to a file. But these methods lack any semantics.

"There's no way to distinguish between encrypted/hashed files with various computational properties. For instance, there is no way to distinguish between that file being a sequence of transactions whose sum is $100, and a song, or a JPEG picture."

"The whole point about things like zero knowledge proofs is that, using them you can argue about various properties of encrypted data without revealing that data" he said.

The ring-shaped cave

A story has been used to explain zero-knowledge protocols, involving a cave shaped like a ring, with the entrance on one side and the magic door blocking the opposite side. In this story, Peggy has uncovered the secret word used to open a magic door in a cave. Victor wants to know whether Peggy knows the secret word; but Peggy, being a very private person, does not want to reveal her knowledge to Victor or to reveal the fact of her knowledge to the world in general.

They label the left and right paths from the entrance A and B. First, Victor waits outside the cave as Peggy goes in. Peggy takes either path A or B; Victor is not allowed to see which path she takes. Then, Victor enters the cave and shouts the name of the path he wants her to use to return, either A or B, chosen at random. Providing she really does know the magic word, this is easy: she opens the door, if necessary, and returns along the desired path.

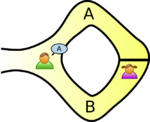
However, suppose she did not know the word. Then, she would only be able to return by the named path if Victor were to give the name of the same path by which she had entered. Since Victor would choose A or B at random, she would have a 50% chance of guessing correctly. If they were to repeat this trick many times, say 20 times in a row, her chance of successfully anticipating all of Victor's requests would become vanishingly small (about one in 1.05 million).

Thus, if Peggy repeatedly appears at the exit Victor names, he can conclude that it is very probable – astronomically probable – that Peggy does in fact know the secret word.

Take, for example, some hash of a big file of all transactions that a bank did in the past year. Now the bank wants to disclose to the authorities that no transactions relates to terrorism or perhaps that it has no accounts that belong to US citizens, or if it does have such accounts then they pay US tax on them.

These are all statements that hold with respect to certain databases and not with respect to others. Using traditional cryptography to prove this stuff, the bank really needs to decrypt the file or de-hash it and show it. But with zero-knowledge proofs it can give you a cryptographically meaningful proof that that property holds without decrypting the file.

Ben-Sasson said this technology can be applied to ascertain any property that can defined by a computer program, such as tax payments: "Say, each transaction has to pay 5% tax, that's a very simple computation to check and prove using ZK proofs.

"You can also use white and black lists with such proofs – say, you can only pay to someone who has been registered at this government office, or you cannot pay any address that appears on this blacklist.

"All of these things can be translated into computations that then can be ascertained and verified in a cryptographic way."

Of course, Bitcoin is a shift from using banks as central trusted third parties. The latter maintain with integrity some ledger of payments, and each customer has an encrypted communication channel to that bank.

In a system such as Bitcoin, basically all information is pretty much public, so all payment amounts and who paid and where they got it from, are public; the only way you hide your identity is by using pseudo identities.

"If an employer were to pay staff with Bitcoins, I could sort of see who is paid on the same day I was paid, or at least know if my payment was average or I'm getting much less than others and so on. This is a problem for Bitcoin because now every employee must either use some extra means to hide his identity or face the prospect of having all his financial transactions deciphered," said Ben-Sasson.

Instead of transactions being in the open, if all you saw was cryptographic commitments nothing could be learned from these. But this presents potential problems concerning computational integrity, because you cannot check whether people have the funds to supply transactions.

"So Zerocash would prove the information encrypted inside one of these transactions; if you decrypt it you would see that the funds being transferred are the same as the funds appearing in a previous unspent transaction and you would see what that previous transaction was and so forth.

"The proof convinces you that payments are legitimate, that the balance is maintained. But you know nothing about where the money came from and who it's going to."

A problem for privacy solutions is scaling them; they tend to be quite computationally onerous, especially running on top of smart contracts on a blockchain, for instance.

Ben-Sasson said ZK proofs definitely take time and computational resources to run, although this would be improved by better engineering and by using more advanced computers. "The proof is like 300 bytes long but to generate it takes roughly 46 seconds. So, it's much longer than it would take you to generate a Bitcoin transaction, which just has a couple of digital signatures and takes less than a second.

"Checking these transactions is still pretty efficient. It takes like 10 milliseconds, so it's more than checking a Bitcoin transaction but it's not horrendous. I should also mention there is a lot of memory consumption required, you need a lot of RAM to generate one of these proofs. We will get these things down, and technology advances – it's not going to stay 46 seconds, but it is always going to be much more costly than Bitcoin."

Ben-Sasson is a scientist and not over-familiar with the world of private blockchains, but he said ZK proofs exist as open source code which can be forked and optimised for various use cases. "I hope that a lot of companies and endeavors use this to start off various private or other kinds of blockchains for other things.

"You would probably want to tweak some of the computations that go underneath. Just like people took Bitcoin, called it something else and used it only for transactions in some gaming community, for example, you could do the same thing."

In terms of the sort of optimisations for scaling to private blockchains, he pointed out that the lab tests were done using a strong server a couple of years ago; using one of today's cutting-edge $20k computer would make things work faster.

He said the number of transactions the system is going to deal with is a big factor. The complexity and the time it will take to generate the proof is proportional to how complicated the computation is itself.

"From the point of view of the ZK proofs, the only thing that matters is the number of gates or computational operations that you need to run the computation from start to end.

"But if you have a very long programme that you want to check; that the derivatives match or bonds have certain properties that have to compute, this can also have an effect."